Mínimo Común Múltiplo
¿Qué es el mínimo común múltiplo o m.c.m.? Vamos a definir cada una de las palabras:
MÍNIMO: no necesita aclaración ¿cierto?
COMÚN: tiene varios significados. Aquí vamos a usar esta palabra como sinónimo de “algo que se repite”. Y para que algo se repita, tiene que estar por lo menos dos veces, lo que quiere decir que vas a tener que usar al menos dos números para realizar la comparación.
MÚLTIPLO: es el resultado de la tabla de multiplicar. Para una explicación más detallada, hacé clic aquí.
Si ahora juntamos la definición de esas tres palabras, sabremos que buscar el mínimo común múltiplo consiste en hallar, entre dos o más números, el múltiplo más pequeño que se repite entre ellos.
Veamos un ejemplo. Si tenés el 4 y el 14, empezá buscando sus múltiplos, hasta encontrar el que tengan en común (resultado que se repite):
4 = 4, 8, 12, 16, 20, 24, 28 (son los resultados de la tabla del 4)
14= 14, 28 (son los resultados de la tabla del 14)
Observá que el primer múltiplo que se repite en ambas tablas, es el 28. Como es el primero que aparece en las dos, es el mínimo.
De modo que m.c.m. = 28
Segundo ejemplo
Usemos ahora tres números. Si tenés el 3, el 6 y el 9, empezá buscando sus múltiplos, hasta hallar el que tengan en común:
3 = 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36.
6 = 6, 12, 18, 24, 30, 36
9 = 9, 18, 27, 36
Aunque el 36 también está en la tabla del 3, 6 y 9, no es el más chico, de modo que el m.c.m. que buscás es el 18.
Procedimiento para calcular el m.c.m. con factoreo
Cuando no es tan sencillo descubrir el m.c.m., por ejemplo, porque los números son muy grandes, existe un procedimiento fácil de realizar:
En primer lugar realizás el factoreo de los números, ya sean dos, tres o más, de la manera que expliqué en este post.
Por ejemplo, si tenés el 20 y el 35, hacés el factoreo y te quedaría así:

¡Concentrate ahora en los números en rojo, que son los que vas a utilizar para calcular el m.c.m.!
Observá que es importante expresar como potencia los factores repetidos.
Comparás los factores del 20 y los del 35 y elegís los factores que se repiten y los que no se repiten. Si se repiten, elegís los que tienen el mayor exponente.
Para resolver este ejemplo, te copio todos los factores de los dos números:

Observá que entre los números recuadrados seleccioné el 7 que no estaba repetido, luego el 5 y el 2 que sí estaban repetidos, con su mayor exponente). Ahora solo te queda usar esos números y realizar la operación:
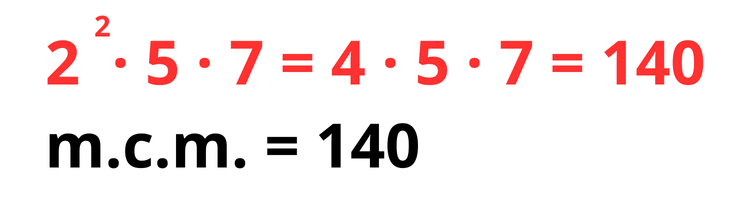
Fijate que tiene sentido que dé ese resultado porque el 140 es el primer múltiplo (resultado) que se encuentra tanto en la tabla del 20 como en la del 35.
Máximo Común Divisor
También lo vas a encontrar con el nombre de Divisor Común Mayor y abreviado como MCD o DCM. No te preocupes, podés usar cualquiera de esas formas para nombrarlo. Vamos a definir cada una de las palabras que lo conforman:
MÁXIMO: ¡no hace falta definirla!
COMÚN: igual que en el anterior, se refiere a aquello que se repite.
DIVISOR: es el número por el que se divide una cantidad. Para saber un poco más, hacé clic aquí.
Si ahora juntamos la definición de esas tres palabras, sabremos que buscar el máximo común divisor consiste en hallar, entre dos o más números, el divisor más grande que se repite entre ellos.
Veamos un ejemplo. Si tenés el 24 y el 16, empezá buscando todos sus divisores:
24 = 1, 2, 3, 4, 6, 8, 12, 24 (son todos los números por los que se puede dividir el 24 y que dan exacto).
36 = 1, 2, 3, 4, 6, 9, 12, 18, 36 (son todos los números por los que se puede dividir el 36 y que dan exacto).
Observá que hay varios divisores que se repiten pero elegís el más grande, que es el 12.
De modo que M.C.D. = 12
Un ejemplo más, usando el 20 y el 7:
Divisores de 20: 1, 2, 4, 5, 10, 20
Divisores de 7: 1, 7.
En este caso, en donde solo tienen el 1 como divisor en común, hablamos de números coprimos. Para más información, te invito a hacer clic aquí.
¿Qué pasa cuando no es tan sencillo darse cuenta cuál es el M.C.D.? Para estos casos, existe un procedimiento sencillo. ¡Prestá mucha atención?
Procedimiento para calcular el M.C.D. con factoreo
En primer lugar tenés que realizar el factoreo de los números, ya sean dos, tres o más, de la manera que expliqué en este post.
Por ejemplo, si tenés el 120 y el 100, hacés el factoreo y te quedaría de la siguiente manera:
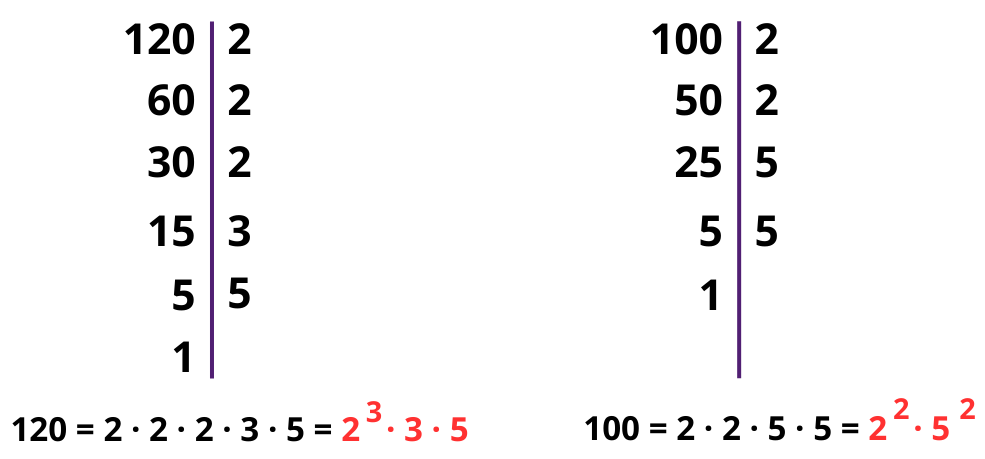
¡Concentrate ahora en los números en rojo, que son los que vas a utilizar para calcular el M.C.D.!
Observá que es importante expresar como potencia los factores repetidos.
Comparás los factores del 120 y los del 100 y elegís solamente los factores que se repiten y si tienen exponente, elegís el que tiene el menor.
Para resolver este ejemplo, te copio todos los factores de los dos números:

Observá que los números recuadrados son los que están repetidos (tanto el 5 como el 2, aparecen dos veces) y elegís de ambos el que tiene el menor exponente (recordá que el 5 que está solo, se hace de cuenta que tiene un 1 como exponente). Ahora solo te queda usar esos números y realizar la operación:
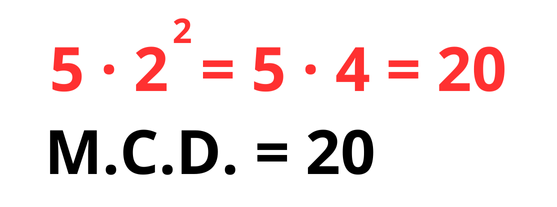
Fijate que tiene todo el sentido del mundo que dé ese resultado, porque 20 es el divisor más grande por el que pueden dividirse tanto el 120 como el 100.